an interesting calculus problem

I should preface this by saying I am in no way advanced in calculus (as I am now taking my first course in it), but while reviewing for an exam a certain beautiful conceptual problem came up. It is given as follows:

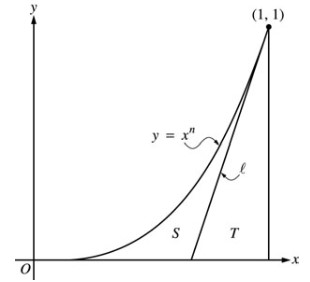
let \(l\) be the line tangent to the graph of \(y = x^n\) at the point (1, 1) where \(n\) > 1 as shown above.

a.) Find \(\int_0^1 x^n \ dx\) in terms of \(n\).

b.) Let \(T\) be the triangular region bounded by \(l\), the x-axis, and the line \(x = 1\). Show that the area of \(T\) is \(\frac{1}{2n}\).

c.) Let \(S\) be the region bounded by the graph of \(y = x^n\), the line \(l\), and the x-axis. Express the area of \(S\) in terms of \(n\) and determine the value of \(n\) that maximizes the area of \(S\).

Part A is a relatively trivial task although I did have to think about it for a little when first solving the problem. In this case, the antiderivative is \(\frac{x^n+1}{n+1}\ + c\). After plugging in the bounds of the intergral we get \(\frac{1^{n+1}}{n+1}\) which is equivalent to \(\frac{1}{n+1}\).

Part B is, in my opinion, the most challenging portion of the problem. It is asking for the area of the triangular region which we know to be \(\frac{1}{2}\ bh\). Our height is 1, but how do we get the base in terms of n? First, we must find the slope of the line \(l\). This is equal to the derivative of \(x^n\) at \(x = 1\). Taking the derivative using the power rule, we get \(nx^{n - 1}\), plugging in \(x = 1\) into this we get the slope of the line \(l\) to be equal to \(n\). So now we have the slope of \(l\), but how does that help us? This is the clever part; using the slope formula \(\frac{y_1 - y_0}{x_1 - x_0}\) we get that \(n = \frac{1 - 0}{x_1 - x_0}\) if we define a variable \(b\) represeting the base of the triangle such that \(b = \Delta x\) we get that \(n = \frac{1}{b}\), solving for \(b\) results in \(b = \frac{1}{n}\). Now we can plug our base value into the formula for an area of a triangle resulting in \(a = \frac{1}{2n}\). Beautiful, isn’t it?

Part C is also interesting as it applies a lot of material learned in Calc 1. The area can be expressed as the equation \(A = \int_0^1 x^n\ dx - A_T\), we know both these values, so plugging them in results in the equation \(A = \frac{1}{n+1} - \frac{1}{2n}\). Taking the derivative of this function we get \(\frac{dA}{dn} = \frac{-1}{(n+1)^2} + \frac{1}{2n^2}\), after setting this equation equal to zero to find the critical points we get \(n = \frac{1}{\sqrt{2}- 1}\).

Overall, I liked this problem a lot and felt it was a good review of nearly every skill learned in Calc 1. I especially loved the slope connections made in part b.

Anyways, bye for now.